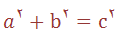
همانطور که می دانیم چنین مثلثی قائم الزاویه است . روشن است که اگر دو تا از این عددها مقسوم علیه مشترکی داشته باشند?عدد سوم هم بر این مقسم علیه قابل قسمت خ.اهد بود .به همین مناسبت در بحث زیر تنها از عددهای صحیحی صحبت خواهیم کرد که مقس.م علیه مشترکی (بجز واحد ) نداشته باشند.

فیثاغورث قاعده ای را به دست اورده بود که طبق آن بتوان عددهای صحیحی برای مثلثهای فیثاغورثی بدست آورد . با علامت گذاریهای امروزی ? این قاعده با تساوی زیر بیان می شود:

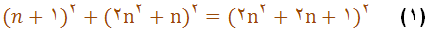
که بجای n می توان هر عدد طبیعی دلخواه قرار داد.

جدول زیر بر اساس این قاعده تنظیم شده است:

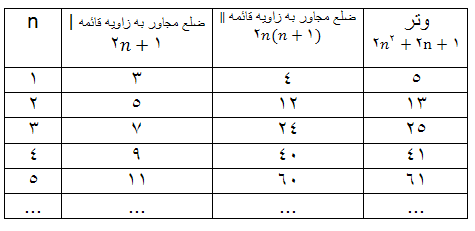
از تساوی (1) و در جدول دیده می شود: عددهایی که ضلع مجاور به ضلع قائمه ? و وتر را معین می کنند? دو عدد متوالی طبیعی هستند.به این تر تیب می توان گفت که اگر در رشته عددهای طبیعی به دو عدد متوالی بر خورد کنیم که مجموع آنها مجذور کامل باشد ? این دو عدد همراه با جذر مجموع آنها? سه ضلع مثلث فیثاغورثی را مشخص می کنند:

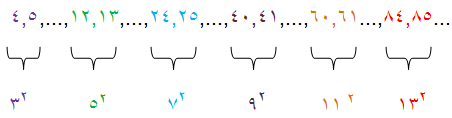
علاوه بر تساوی (1) ?تساویهای دیگری هم برای معین کردن عددها فیثاغورثی وجود دارد که دیر تر پیدا شده است.

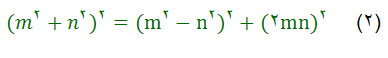
در این رابطه می توان بجای mوnهر عدد دلخواه صحیح قرار داد. مثلا اگر m=3 وn=1بگیریم بدست می آید:

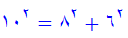
یعنی تر کیبی از عددهای 6?8,10 بدست می اید که در جدول قبل وجود نداشت. به همین مناسبت رابطه (2) کلی تر از رابطه (1) به نظر می رسد.

ولی مطلب از این جدی تر است.رابطه (2) شامل تمام انواع ممکنه عددهای سه گانه فیثاغورثی است. اگر بخواهیم مثلثهای متشابه فیثاغورثی تکرار نشود (مثلا دو مثلث 3?4?5 و 6?8?10 متاشابه اند.)باید قاعده های زیر را رعایت کنیم:

1) از دو عدد mوn باید یکی فرد و دیگری زوج باشد?

2) باید دو عدد mوn نسبت به یکدیگر اول باشند? یعنی مقسوم علیه مشترکی بجز واحد نداشته باشند?

3)

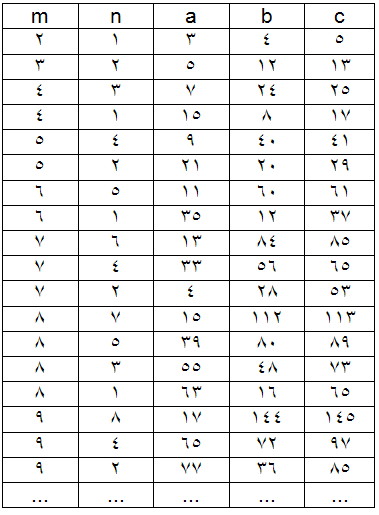
جدولی را که در آن این قاعده ها رعایت شده است ? در زیر می آوریم: